Environment 121: Conservation of Biodiversity

Lecture topic: Demography of small populations

17 April 2007

Conservation in the news

• Climate Change Worries Military Advisers (April 16, 2007, National Public Radio)

Outline of lecture:

I. Review of population growth models

Density-independent population growth models

Density-dependent population growth models

Age-structured, density-independent population models

Stage-structured, density-independent population models

II. Special cases for small populations

III. Advanced concepts for small populations

I. Review of Population Growth Models

Density-independent population growth models

A. Discrete generation

1. Assumptions

• Live, reproduce once, die
• No competition or other density-dependent factors
• Birth and death rate are constant
• No immigration or emigration

2. Definitions

• For single generation, size of next generation (N_t+1) is a function of the current population size (N_t)) at time "t"', multiplied times number of female offspring born minus number of females that died. Or,

  

• Where R₀ = average number of female offspring produced per female that survives until next generation and

  R₀=N_t+1 / N_t

To project population under the assumptions of this model:

N_t = N₀ R₀^t

R > 1 => population is growing

R = 1 => population size is constant

R < 1 => population is declining

When would density-independent growth be applicable to conservation cases?
Perhaps invasive species.

B. Continuous growth

1. Assumptions

a. Same as above

b. Both discrete and overlapping generations grow exponentially, when growth is positive

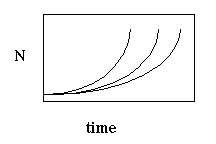
2. Definitions

a. Change in population size can be defined as:

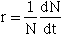
--where r is referred to as the intrinsic rate of increase

b. r = b - d where b = instantaneous birth rate and d = instantaneous death rate



• r > 0 ==> population is increasing
• r = 0 ==> population is constant, no growth
• r < 0 ==> population is decreasing

3. Logistic equation is derived from above equation:

4. Calculation of r:

a: Using the equation below, plot N versus t on semi-log paper.

b. Slope is r.

c. Notice:



 

Density-dependent population growth models

A. Verhulst (1838) equation

1. Note that change in population size is a function of N and K.

2. Known as logistic equation

3. Integrated form of equation :



 

4. Change in population is at its maximum at intermediate population size. (see example below)

5. Allele effect occurs at low N

Example: Bacteria population with K=100, r=1.0, N₀=1

 

Population size (Nt)	(K-N)/K	dN/dt (rate of pop. growth)
1	.99	.99
50	.50	25.0
75	.25	18.75
95	.50	4.75
99	.01	.99
100	.00	0

Note that the change in population growth rate over time is fastest at intermediate population sizes.

Issues for conservation:

• Carrying capacity can be reduced by landscape change
• Carrying capacity can be reduced by competition from other species, such as invasive species.
• Disturbance can affect “r”, (examples?)

Age -structured models (density independent)

A. Life tables

1. Definition: age-specific mortality schedule of a population

2 Critical parameters:

a. age interval

b. age specific survival

c. age specific fecundity

3. Example

age, x	Number of individuals	survival, lx	age-specific survival, lx	age-specific fecundity
0	150	1.0	.5	0
1	75	.5	.4	1.5
2	30	.2	0	2
3	0	0

3. Types of life table

a. Cohort: generational; survivorship based on a single cohort over time.

b. Static (vertical): survivorship based on multiple age classes sampled at one point in time.

c. modified cohort: cohort of individuals is monitored for 1-many years.

4. Information estimated from life tables:

a. age-specific life expectancy: average number of years to live for an individual of age x.

b. age-specific reproductive value: Relative number of offspring that remain to be born to individuals of a given age.

c. Net Reproductive Rate (R₀) average number of female offspring produced by each female during her lifetime.



 

B. Population matrices

1. Life table information is summarized into a matrix



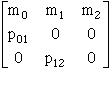
2. Using data from example above, we can construct the following matrix.

3. Using matrix algebra, we can calculate the population growth rate: determine that the following matrix has

l = e^r = 1.0615

r=ln l = 0.0597

 

IV. Stage structured population models (density independent)

A. Life table information

1. stages in organisms life

a. insect: egg, pupa, n-star

b. birds: eggs, fledglings, juveniles, non-reproductive adults, reproductive adults

c. Plant: seed stage, seedling stage. sapling stage. juvenile, adult

B How to collect data:

1. Modified cohort

a. Parameters are measured yearly at appropriate time

b. Summarized in terms of stage-specific transition probabilities.

2 . Example of stage-structured data

stage	probability of going to next stage	probability of staying in same stage	stage-specific fecundity
seeds	.50	0	0
seedlings	.20	.40	0
saplings	.25	.50	0
juveniles	.10	.70	10
adults	0	.95	100

C. Stage projection matrix

1. Constructs a matrix from transition probabilities

2. Matrix from table above:

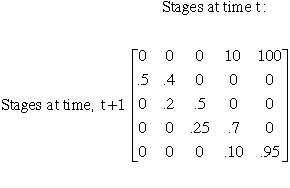
3. Dominant eigen value of this matrix = l = 1.3845

Applications of life table approach for conservation:

Focus on critical phases in life cycle where impact of disturbance is occurring most dramatically

1. Black agouti:  seed disperser/seed predator
• loss of seed dispersers changes seedling recruitment
• 
2. Increase in nest predators on edges: Female cowbird:  nest predator

PHOTO BY taken from http://www.sfu.ca/biology/faculty/williams/ebird/credits.html

See article on Nest predation by cowbird: UC Berkeley News http://www.berkeley.edu/news/media/releases/2004/08/05_cowbird.shtml

II.  Special cases for small populations

 Allee effect:

1. When population is large, positive relationship between population density and the reproduction and survival of individuals

2. When population is small, increased difficultly of finding mates or reproducing at low population size.

3. A special form of density-dependence

Example 1:  African Wild dog

• Tightly knit social groups
• Hunt cooperatively;  approach a herd and chase one individual until it's exhausted. 
• Prey:  grazing animals such as gazelles, springboks, wildebeest and zebras.
• Mating: cooperative breeding with need for helpers creates Allee effect

Example 2:  Self-incompatibility in plants

Aster furcatus , Forked aster: understory plant: found at fewer than 50 sites in six Midwest states, is classified as threatened in Illinois.

Gentiana pneumonanthe, European understory shrub.

Both species have incompatibility systems:

• plant cannot mate with self or individuals with same allele at the s-locus.
• Problematic for isolated, small populations.

III. Advanced concepts for small populations

A.  Demographic uncertainty

1. random events in survival and reproduction of individuals.
2. skewed sex ratio
3. random sequence of deaths
4. mainly effects small populations
5. Can cause variance in R or r from  year to year, which reduces population size

B. Environmental uncertainty or stochasticity

1. Defintion: changes in weather, food supply, and the populations of competitors, predators and parasites
   • affects populations of all sizes
   • Can create density-independent conditions
2. Natural catastrophes
3. Extreme cases of environmental uncertainty
4. Infrequent, short in duration, widespread in impact